Back
Sieve: SAEs Beat Baselines on a Real-World Task (A Code Generation Case Study)
Key Results
- We demonstrate the first application of SAE-based interventions to a downstream task that outperforms classical baselines with minimal effort/time.
- We develop an end-to-end pipeline for applying SAEs for fine-grained control, which we term Sieve.
- The task, obtained directly from a YC startup: Reliably generating fuzz tests for Python functions while avoiding specific patterns like regex usage.
- Baselines/other approaches include prompt engineering and steering vectors, which are inconsistent and require extensive tuning. The SAE method was the simplest and easiest to implement.
- By using an SAE, we do conditional feature steering that precisely prevents regex usage while maintaining model performance.
- Unlike system prompts, fine-tuning, or steering vectors which affect all outputs, our method is very precise (>99.9%), meaning almost no side effects on unrelated prompts.
 Our methods achieve Pareto dominance on the axis of task success rate vs task constraint satisfaction vs general model performance.
Our methods achieve Pareto dominance on the axis of task success rate vs task constraint satisfaction vs general model performance.
Mechanistic Interpretability and Sparse Autoencoders
Mechanistic interpretability aims to explain the internal mechanisms of models from the weights of the model alone. However, this goal is complicated by behavior like superposition[1]. In superposition, rather than each neuron representing one set of semantic features, dissimilar features emerge from combinations of neurons firing together. One promising way of overcoming this is via sparse autoencoders (SAEs)[2], a fully unsupervised approach whereby one learns a large linear “dictionary” of monosemantic, interpretable features that exist in the model. The key idea is that by encouraging sparsity in the right way, we can obtain more interpretable and meaningful features.
Concretely, SAEs learn a dictionary of encoder and decoder vectors that first map representations in the model’s activation space (its “information highway”) to a sparse latent space of features and then use these sparse latents to reconstruct the original representation respectively.
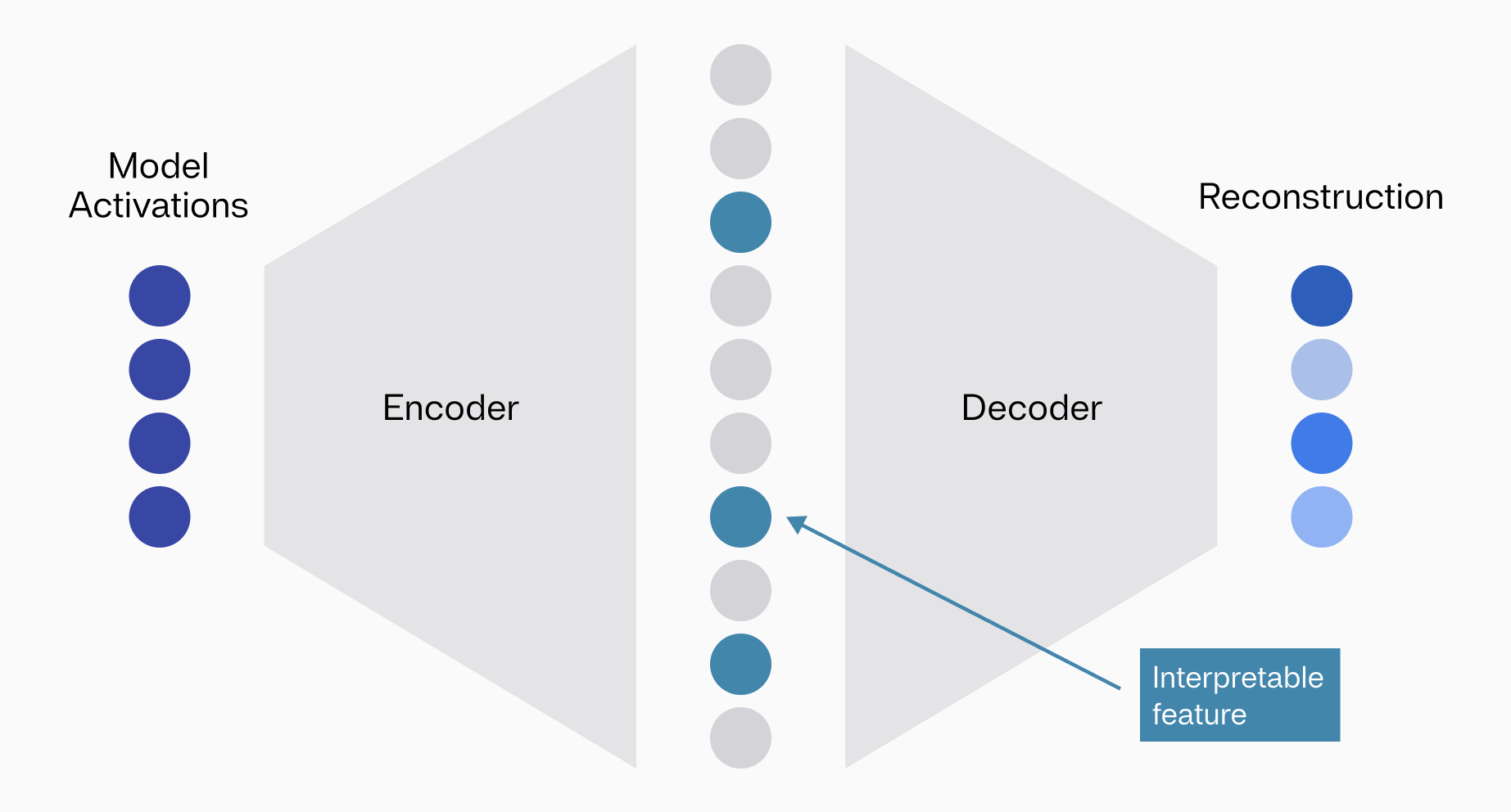 Depiction of the encoder-decoder process in an SAE.
Depiction of the encoder-decoder process in an SAE.
Mathematically, this is represented as
Where is either:
- TopK[3]: Selects the top activations
- JumpReLU[4]:
For more intuition about SAEs, we recommend checking out our previous blog post[5] and Adam’s blog post[6].
SAEs are compute-intensive (typically, the sparse latent space is a much higher-dimensional space than the original activation space), but when trained, they offer tens of thousands of generalizable conditional levers on model behavior. As such, they offer unique customizability and steerability of models at inference time.
While SAEs have uncovered novel facets of model behavior through interpretability [7] [8], to date, they have not been applied to a downstream use case that counterfactually enables a certain application. In this post, we describe our investigations into the first concrete application of SAEs that outperforms traditional baselines (such as prompting and steering vectors).
Remarkably, we achieved these results with minimal engineering effort - the entire implementation took less than 15 minutes using standard tools like HuggingFace Transformers. This demonstrates that SAE-based interventions aren't just theoretically interesting, but are now practical, production-ready tools that practitioners can easily deploy to solve real model control problems. For teams struggling with model control issues, our results suggest that, in certain situations, SAEs could be the first solution they reach for, not the last.
Task Setup
The task we analyzed was given to us by Benchify, a YC code-gen company, and is similar to a real application case of their product (with the specifics slightly modified to protect IP). The objective is to write code to reliably fuzz test the given Python function. Fuzz tests involve feeding unexpected inputs to a program to uncover bugs and vulnerabilities.
The setup consists of:
- A real system prompt: Copy-pasted from Benchify’s product, the prompt contains detailed instructions, example code snippets, specifications, and constraints.
- Behavioral constraints: The AI model must avoid certain generations, such as not using “self” as these are standalone tests that are not part of a test class.
- The constraint we target is avoiding usage of regexes (strings for text pattern matching).
- We want to generate tests that don't generate false positive errors. Benchify observed that the model was much more likely to generate a test with no false positives when using string methods instead of regexes, even if the test coverage wasn't as extensive.
 For demonstration purposes only. Note that the non-regex solution is less expressive, but this is a tradeoff we are willing to make to avoid false positive errors.
For demonstration purposes only. Note that the non-regex solution is less expressive, but this is a tradeoff we are willing to make to avoid false positive errors.
The main challenges here lie in:
- Producing valid, executable test cases.
- Respecting the constraints while still exploring diverse edge cases.
- Outperforming traditional baselines, such as prompt engineering or steering vectors, in reliability and coverage.
- Maintaining base model performance without hijacking the representations the model may use for other tasks.
Why is this hard?
System prompts often fail in long contexts in multi-step constrained tasks[9][10]. The Benchify system prompt consists of a complex set of constraints and an extensive amount of documentation about their internal tooling, which the model must balance precisely. Moreover, the nature of the function to be fuzz-tested can cause the LLM to heavily prefer a certain implementation strategy (e.g., using regexes for string matching tasks).
Prompt engineering can mitigate this in short context inputs. However, Benchify frequently has prompts with greater than 10,000 tokens, and even frontier LLMs like Claude 3.5 will ignore instructions at these long context lengths. In addition, edits made to emphasize a certain set of constraints come at the cost of creating a "whack-a-mole" problem - fixing one issue frequently causes new problems or undoes previous fixes.
 The first snippet undesirably uses regex, while the second avoids regex but introduces improper use of self, coupling the function to a class unnecessarily.
The first snippet undesirably uses regex, while the second avoids regex but introduces improper use of self, coupling the function to a class unnecessarily.
The technical challenge for our method is then as follows:
- High precision-recall of detection to minimize interference with unrelated tasks, preventing potential “whack-a-mole” problems.
- A targeted, strong intervention that fully ablates violating behavior in the model while maintaining code functionality.
- Facility of the method: Any such fix should require minimal additional effort/data from the practitioner.
To satisfy 1) and 2), we hypothesized the need for conditional interventions [11]. That is, we learn both a threshold to determine when in the generation to intervene and a perturbation, which shifts model behavior in a desired direction once the threshold is met.
Baselines
Beyond prompting, we employ two baselines: steering vectors and linear probes. A steering vector w is a vector engineered from contrastive data D whereby adding w to the model’s hidden state coerces the model into behaving similarly to that of a particular subset of D. For example, D could consist of pairs (x,y) where x is a happy or positive passage, and y is a similar passage but written in a sad tone, and one creates a steering vector from this to make the model output more upbeat generations.
The common method for generating a steering vector, which we also employ, is Contrastive Activation Addition (CAA) , following the methodology of Stolfo et al[12] (see Appendix G). Although steering vectors are effective for simple forms of model control, we (and others[13]) have found that constantly applied steering vectors have major side effects, as measured by e.g. MMLU[19]. Nonetheless, we include them as a principled baseline in our analysis.
The traditional detection baseline employed is the linear probe[14]. The probe was similarly extracted from a synthetically generated corpus of positive and negative examples and used as a classifier. Details can be found in Appendix H.
Of note, for the aforementioned baselines, the synthetic data was generated directly using the system prompt we tested on - minimizing the domain shift from train to test. By contrast, the data used to train the SAE did not include any trace of similar data or long regex system prompts (~1% of the data mixture consisted of regex with mostly simple, short examples). We found that even when given this strong advantage, the baselines still fall short of our method.
Problem Setup
We consider three models:
- Gemma-2-2B-IT[15],
- Gemma-2-9B-IT[15],
- Llama-3.1-8B-Instruct[16].
For the former, we use the GemmaScope[17] SAEs trained by Google Deepmind. For the latter, we train Sieve, a suite of lightweight code-specific SAEs from scratch on deduplicated publicly available high-quality coding datasets (~9 A100 hours). For each model, we use automated interpretability[18] to identify a feature candidate for regex intervention (< 5 minutes to search). We then utilized the target feature at generation time as part of an intervention (illustrated below). Crafting the interventions was also an extremely lightweight process with minimal overhead at inference and took < 10 min to implement both with base HuggingFace Transformers or with TransformerLens from start to finish.
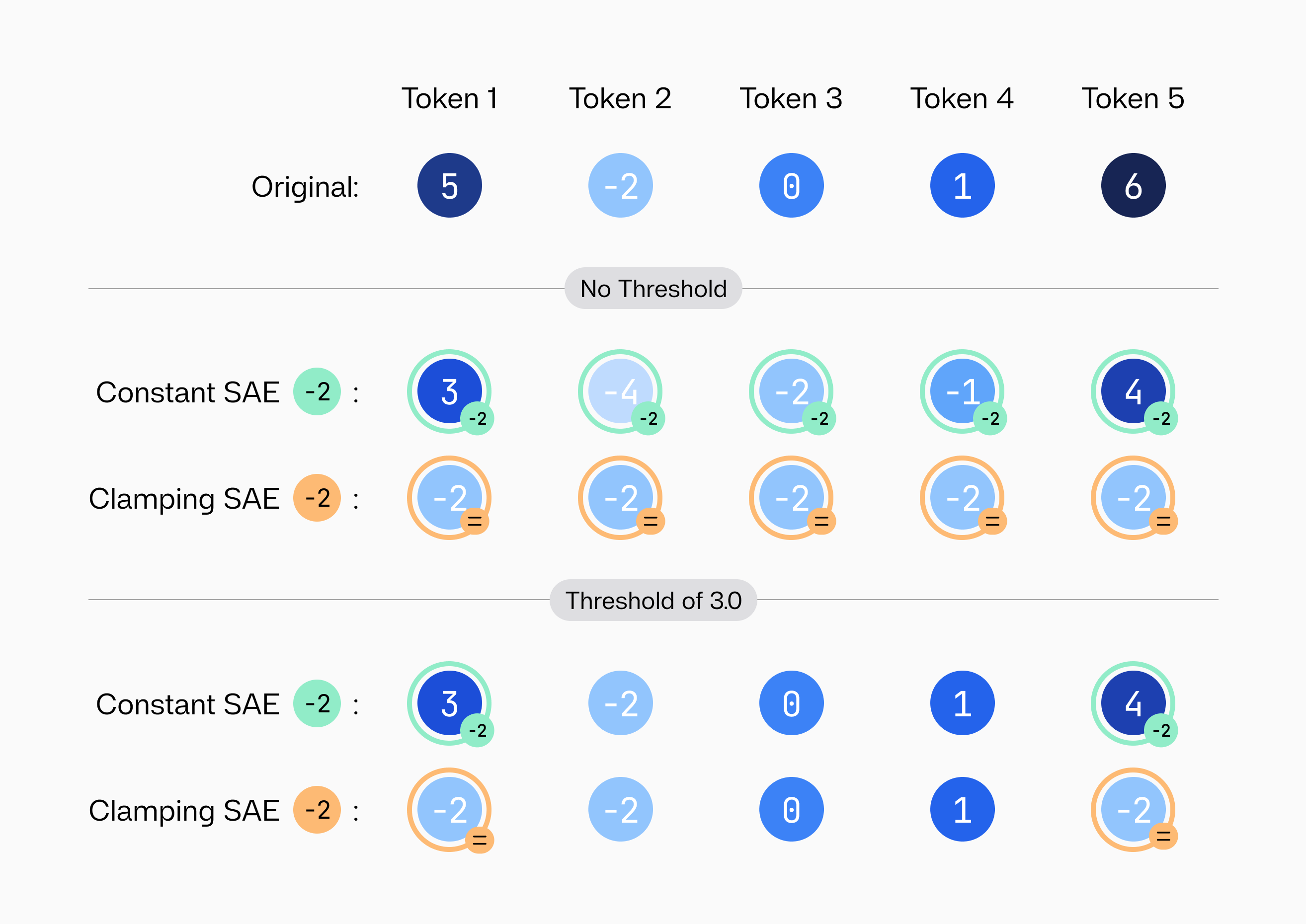 Four examples of SAE interventions and how they affect latent values.
Four examples of SAE interventions and how they affect latent values.
We then ran generations against seven sample Benchify functions to fuzz test, sampling over 100 times per function. We swept across
- strengths for each intervention,
- variations of the system prompt and documentation,
- variations of the target function.
The three primary metrics we evaluated were as follows, with further details in Appendix E.
- Semantic validity: Does the generated function actually fuzz-test the original code?
- Regex usage: Does the model invoke any regex functionality?
- MMLU scores[19]: Does the intervention compromise general model performance?
The fourth metric we considered was time. For Benchify, ease and iteration time for implementation were critical requirements for any sophisticated modification. Whereas SAE-based interventions took ~15 minutes to set up, extracting good contrastive activation vectors or probes took over ten hours of experimentation, especially given how sensitive these methods are to the choice of data and implementation specifics. The performance of the linear probe can be increased by curating a larger dataset but creating a dataset that matches the diversity of the billions of tokens the SAE was trained on is very non-trivial.
Though SAEs require an upfront compute cost, researcher hours at iteration time are much more expensive than a couple dozen GPU hours. In some cases, pre-trained SAEs are also readily available, such as the Gemma Scope series. This cost can additionally be amortized if multiple features from a single SAE for different downstream applications (9 hours for 16384 features comes out to roughly 2 sec/feature).
Results
In this section, we will showcase the features we identified, sample generations, and the results of our evaluations. We found that SAE-based feature engineering achieved Pareto dominance over traditional baselines with little-to-no tuning.
Identifying Features
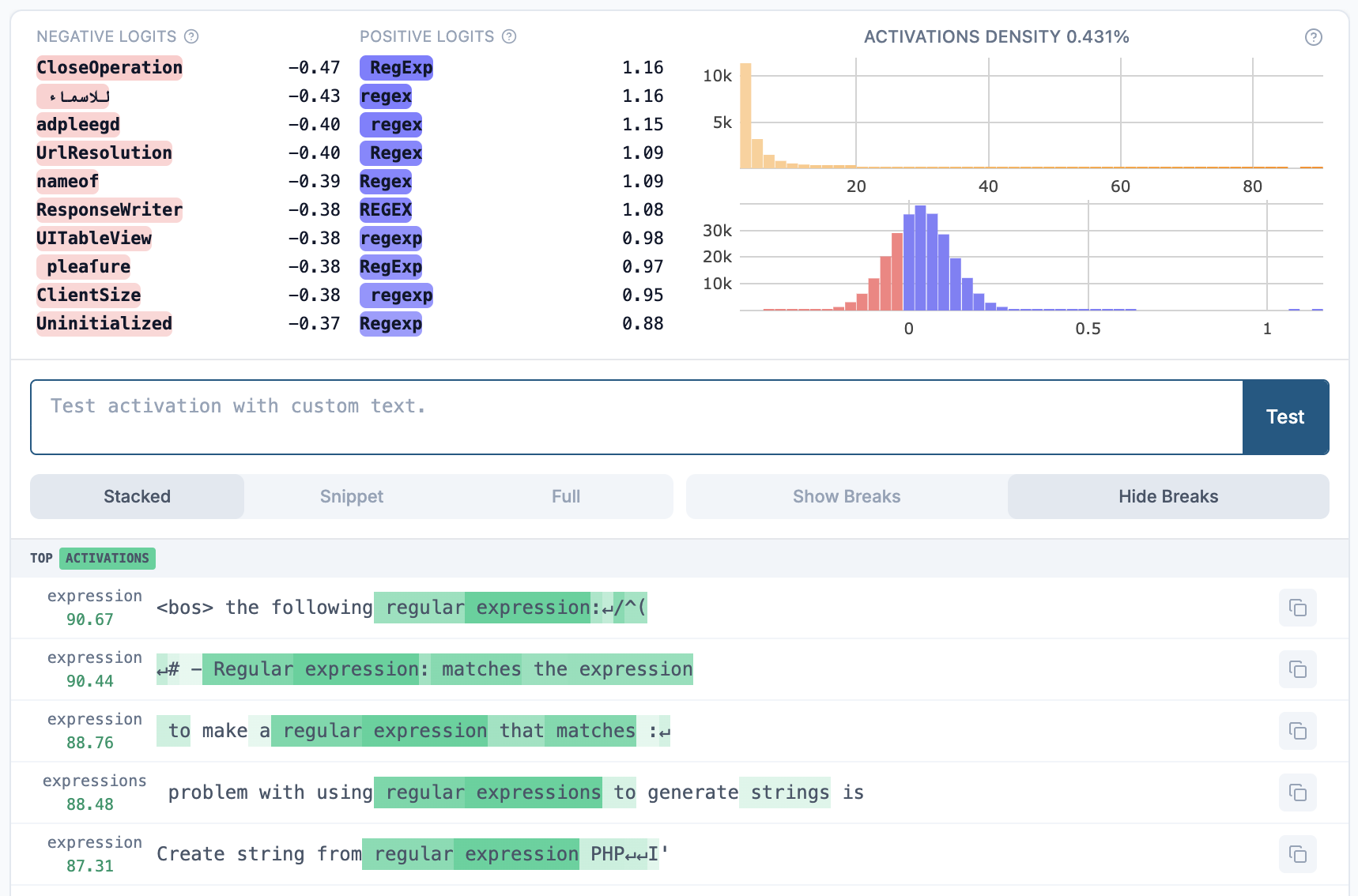 GemmaScope 9B-IT’s regex feature via Neuronpedia’s feature viewer.
GemmaScope 9B-IT’s regex feature via Neuronpedia’s feature viewer.
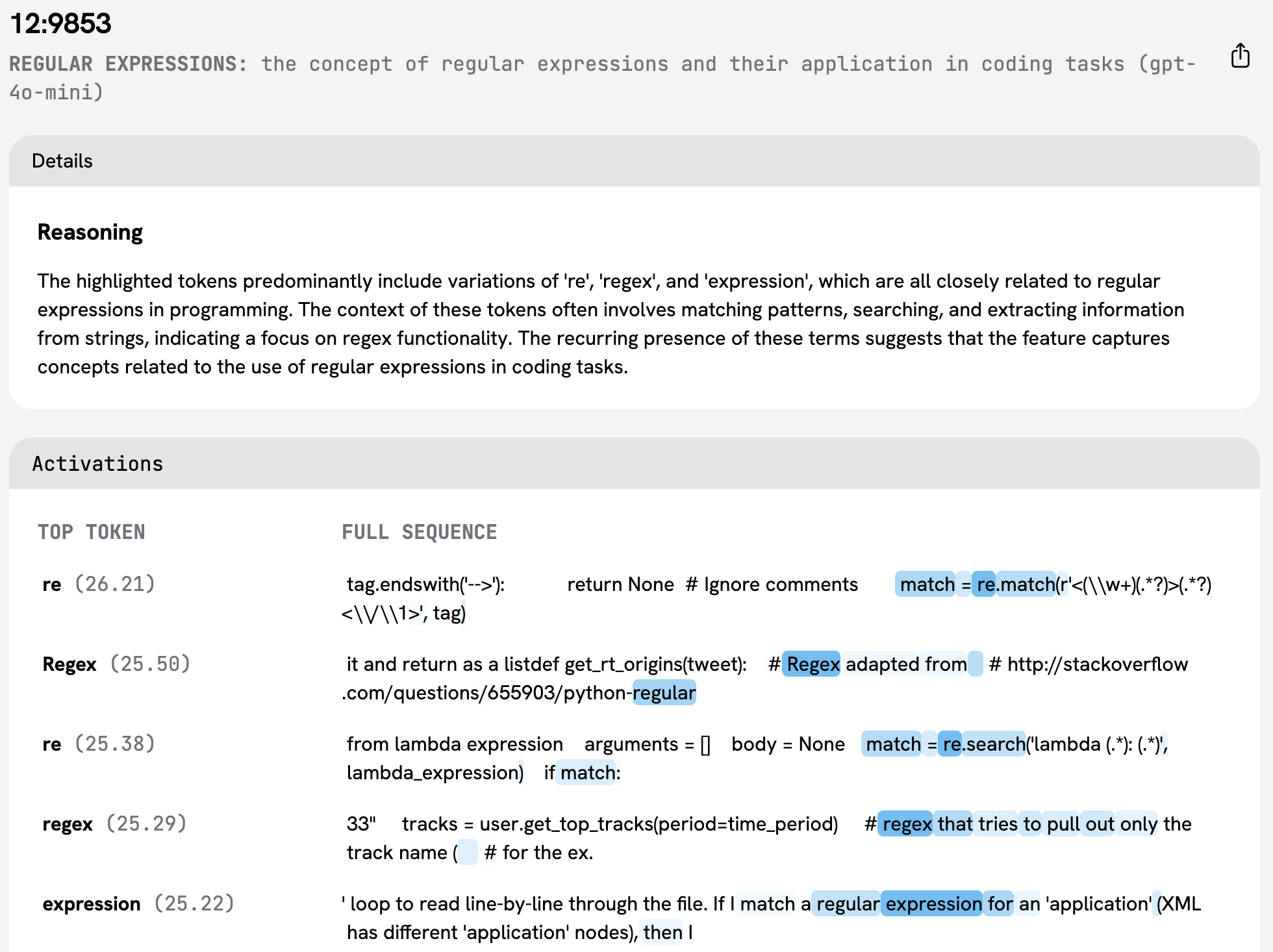 Feature for "the concept of regular expressions and their application in coding tasks", from the layer 12 Sieve SAE.
Feature for "the concept of regular expressions and their application in coding tasks", from the layer 12 Sieve SAE.
Identifying features from the GemmaScope SAEs took < 5 minutes. For example, GemmaScope 9B IT had only a single regex feature! By contrast, the sieve SAEs had roughly 50 regex features each due to the focus on coding data, and identifying a candidate feature for each layer took 15 minutes. The process mainly consisted of studying top activating examples and pattern-matching with the known regex failure modes of the base model.
Sample Generation
 Example generations with and without Sieve conditional interventions.
Example generations with and without Sieve conditional interventions.
Pareto Analysis
We generated Pareto plots for regex rate versus the metrics of semantic validity and MMLU score for different models/configurations. We relegate the majority of plots to Appendix B but we show one Pareto plot per model here to exemplify the general trend.
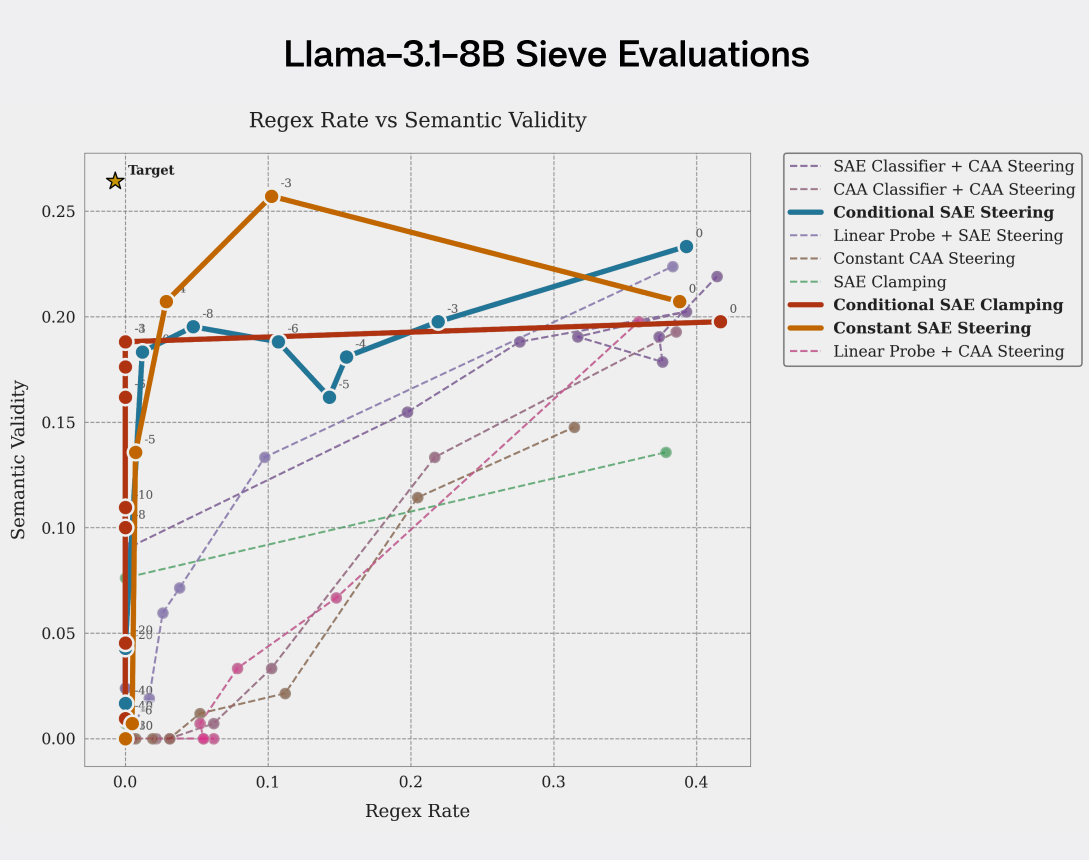
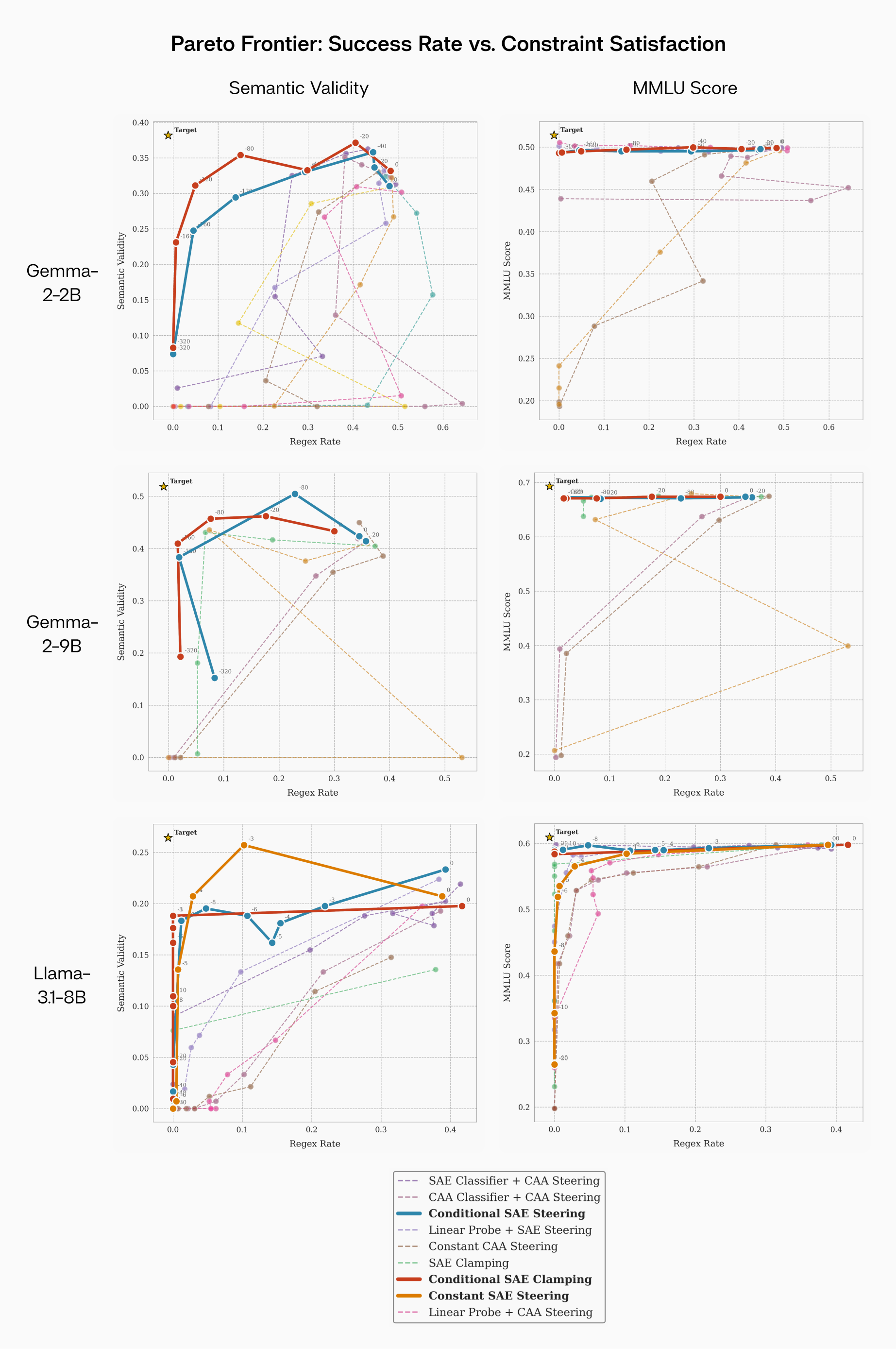 FIGURE 1: Results for Llama-3.1-8B-Instruct on layer 12 and Gemma-2-2B-Instruct on layer 8. SAE-based conditional clamping/steering is dominant.
FIGURE 1: Results for Llama-3.1-8B-Instruct on layer 12 and Gemma-2-2B-Instruct on layer 8. SAE-based conditional clamping/steering is dominant.
Conditional SAE clamping fully eliminates regex usage in Llama with almost no impact on Semantic Validity or MMLU score, demonstrating clear Pareto dominance in Gemma-2-2B-it. Non-conditional interventions produce major side effects on MMLU performance.
A few further observations:
- Whereas the constant SAE intervention on Gemma-2-2B damages both Semantic Validity and MMLU performance, the intervention has less impact on Llama's semantic validity (see Appendix I).
- Counterintuitively, increasing the intervention strength sometimes increases the regex rate (see Appendix J).
- The plots focus on relatively short context inputs, mimicking the synthetic dataset we used to create our CAA steering vector. We find even stronger results in long context regimes (see Appendix D).
- Conditional CAA and linear probe steering results vary from model to model, but MMLU is very out of distribution compared to the CAA training datasets. For some models, they generalize correctly, causing minimal MMLU side effects. For other models, they generalize poorly, with major MMLU side effects.
While our MMLU results for linear probes and CAA conditional steering vary across models, we believe these metrics primarily test out-of-distribution generalization - a property highly sensitive to dataset specifics rather than method fundamentals. More compelling is the precision comparison: even on tasks more similar to the training distribution of our linear probes and CAA vectors, SAE-based methods achieve superior precision (>99.9%) in regex detection. While MMLU is useful for measuring unintended side effects, the high precision of the SAE is a more direct measure of avoiding unintended consequences.
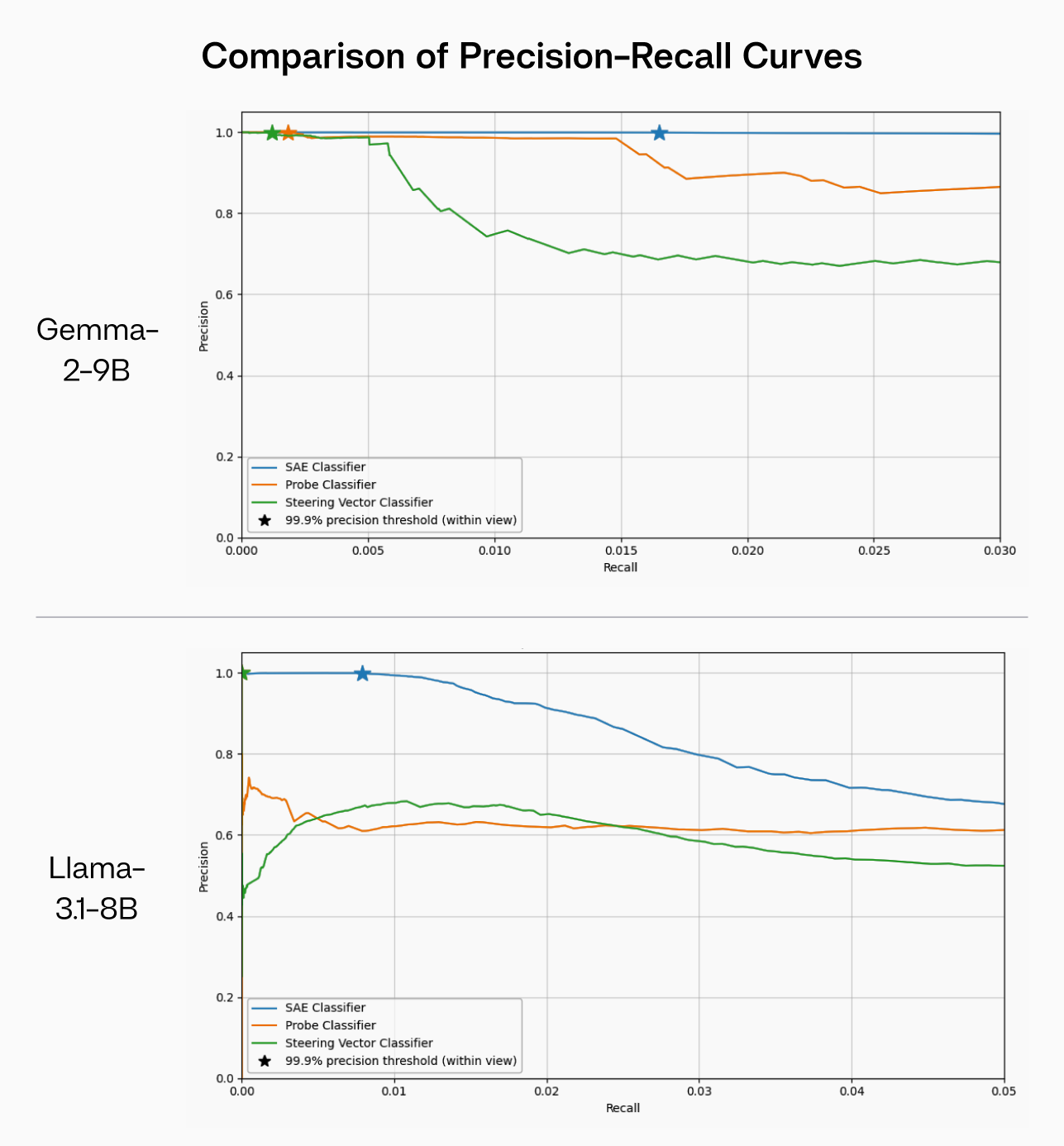 FIGURE 2: Precision-recall curves for different conditional regex classifiers on a held-out dataset of activations for both Gemma-2-9B-IT and Llama-3.1-8B-Instruct. The SAE encoder vector dramatically outperforms both the linear probe and steering vector as a binary classifier, allowing for a significantly higher recall while maintaining high precision (>= 99.9%).
FIGURE 2: Precision-recall curves for different conditional regex classifiers on a held-out dataset of activations for both Gemma-2-9B-IT and Llama-3.1-8B-Instruct. The SAE encoder vector dramatically outperforms both the linear probe and steering vector as a binary classifier, allowing for a significantly higher recall while maintaining high precision (>= 99.9%).
We again want to highlight the importance of conditional SAE clamping/steering here. Unlike fine-tuning, system prompts, CAA steering vectors, and other methods that modify every forward pass, conditional SAE clamping/steering activates only when specific features are detected above a certain threshold. We found that, unlike other methods, SAEs were very precise. They successfully reduced regex usage while activating with a precision of over 99.9%. This allows for the model to be completely unaffected during standard usage on downstream tasks, which is a uniquely strong property for an activation-level safeguard. We present further analysis in Appendix F.
Importantly, SAE-based interventions are not task-specific. A conditional intervention framework can be extended to any complex set of constraint-based instruction-following tasks. We focus on regex here because of Benchify's needs and the clear metrics of success, but in the future, we want to release work generalizing our methods to harder and more complex tasks.
Limitations
The primary limitation of SAE-based clamping/steering is that it relies on the SAE containing a feature that aligns with your desired concept. This will not always be the case. However, using web-based tools like Neuronpedia, we can quickly test the feasibility of SAE-based interventions. In our case, we initially validated the effectiveness of regex steering on Neuronpedia in less than 10 minutes. Thus, there’s minimal risk when experimenting with these tools.
We can increase the likelihood of an SAE containing a desired feature by modifying its dataset composition. Some Gemma-Scope SAEs contained only a single regex feature. In contrast, our Llama SAEs were trained primarily on code data and contained 50+ regex features. There has also been promising work[8] on automatically composing SAE features into a desired vector.
Our work currently only covers smaller models, and we have not yet conducted experiments on larger models like Llama-3.3-70B. However, Benchify has observed that all models they use (Claude 3.5 Sonnet, GPT-4o, and Llama-3.1-70B) suffer from these issues on long context inputs.
Lastly, in this work we limit ourselves to a single task to thoroughly explore many baselines. We plan on exploring a wider range of tasks in the future.
Conclusion
Applied interpretability enables precise and powerful model control for practitioners. However, we posit that a lack of application to meaningful downstream tasks and benchmarking against traditional baselines have hindered the adoption of interpretability. We demonstrate the first applied setting wherein SAE-based interventions achieve better constraint satisfaction without compromising performance for a fraction of the time and effort. This is the tip of the iceberg, and we are excited to expand the potential of applied interpretability.
Our results show that the gap between theoretical interpretability research and practical applications is closing rapidly. We are excited to release further developments towards fine-grained levers for model control, enabled by mechanistic interpretability.
Acknowledgments, Contributions, & Reproducibility Statement
We thank Arthur Conmy, Neel Nanda, and Stephen Casper for their comments and suggestions during the drafting process (listed chronologically). The original idea and task were conceived by Adam and derived from Benchify. Adam and Dhruv developed the infrastructure for interventions and analysis. Steering vector baselines were implemented by Adam, and probe-based baselines were developed jointly by Adam and Dhruv. Adam collected results on the Gemma Suite of models. Mason and Dhruv trained, integrated, and evaluated the Llama sparse autoencoders. Ben, Mason, Dhruv, and Adam collaborated on drafting and revising the manuscript.
As part of our mission towards open science and reproducibility, we are releasing the full harness, data, eval results, and models used in our analysis for researchers (see Appendix A). If you find any of these resources useful, please cite them as follows:
@article{karvonen2024sieve,
title={Sieve: SAEs Beat Baselines on a Real-World Task (A Code Generation Case Study)},
author={Karvonen, Adam and Pai, Dhruv and Wang, Mason and Keigwin, Ben},
journal={Tilde Research Blog},
year={2024},
month={12},
url={https://www.tilderesearch.com/blog/sieve},
note={Blog post}
}
References
- Elhage, Nelson and Hume, Tristan and Olsson, Catherine and Schiefer, Nicholas and Henighan, Tom and Kravec, Shauna and Hatfield-Dodds, Zac and Lasenby, Robert and Drain, Dawn and Chen, Carol and Grosse, Roger and McCandlish, Sam and Kaplan, Jared and Amodei, Dario and Wattenberg, Martin and Olah, Christopher (2022).
- Bricken, Trenton and Templeton, Adly and Batson, Joshua and Chen, Brian and Jermyn, Adam and Conerly, Tom and Turner, Nick and Anil, Cem and Denison, Carson and Askell, Amanda and Lasenby, Robert and Wu, Yifan and Kravec, Shauna and Schiefer, Nicholas and Maxwell, Tim and Joseph, Nicholas and Hatfield-Dodds, Zac and Tamkin, Alex and Nguyen, Karina and McLean, Brayden and Burke, Josiah E and Hume, Tristan and Carter, Shan and Henighan, Tom and Olah, Christopher (2023).
- Gao, Leo and la Tour, Tom Dupr{'e} and Tillman, Henk and Goh, Gabriel and Troll, Rajan and Radford, Alec and Sutskever, Ilya and Leike, Jan and Wu, Jeffrey (2024).
- Rajamanoharan, Senthooran and Lieberum, Tom and Sonnerat, Nicolas and Conmy, Arthur and Varma, Vikrant and Kramár, János and Nanda, Neel (2024).
- Pai, Dhruv and Wang, Mason and Keigwin, Ben (2024).
- Karvonen, Adam (2024).
- Eoin Farrell and Yeu-Tong Lau and Arthur Conmy (2024).
- Sviatoslav Chalnev and Matthew Siu and Arthur Conmy (2024).
- Shawn Gavin and Tuney Zheng and Jiaheng Liu and Quehry Que and Noah Wang and Jian Yang and Chenchen Zhang and Wenhao Huang and Wenhu Chen and Ge Zhang (2024).
- Li, Tianle and Zhang, Ge and Do, Quy Duc and Yue, Xiang and Chen, Wenhu (2024).
- Bruce W. Lee and Inkit Padhi and Karthikeyan Natesan Ramamurthy and Erik Miehling and Pierre Dognin and Manish Nagireddy and Amit Dhurandhar (2024).
- Alessandro Stolfo and Vidhisha Balachandran and Safoora Yousefi and Eric Horvitz and Besmira Nushi (2024).
- Braun, Joschka and Krasheninnikov, Dmitrii and Anwar, Usman and Kirk, Robert and Tan, Daniel, and Scott Krueger, David (2024).
- Alain, Guillaume and Bengio, Yoshua (2016).
- Gemma Team (2024).
- Llama Team (2024).
- Tom Lieberum and Senthooran Rajamanoharan and Arthur Conmy and Lewis Smith and Nicolas Sonnerat and Vikrant Varma and János Kramár and Anca Dragan and Rohin Shah and Neel Nanda (2024).
- Bills, Steven and Cammarata, Nick and Mossing, Dan and Tillman, Henk and Gao, Leo and Goh, Gabriel and Sutskever, Ilya and Leike, Jan and Wu, Jeff and Saunders, William (2023).
- Dan Hendrycks and Collin Burns and Steven Basart and Andy Zou and Mantas Mazeika and Dawn Song and Jacob Steinhardt (2021).
Appendix
A. Reproducibility
We provide comprehensive resources to ensure full reproducibility of our results:
Pre-trained SAEs
- GemmaScope SAEs: Available on HuggingFace at
google/gemma-scope - Sieve SAEs: Available on HuggingFace at
tilde-research/sieve_coding
Code and Implementation
- Source Code: Available on GitHub at
tilde-research/sieve
Evaluation Results
- Full Evaluation Data: Available in our Google Drive repository
2b_probes_data.zip(86 MB)9b_sieve_evals_v1.zip(22.1 MB)llama_sieve_evals.zip(101.2 MB)
All resources are publicly accessible. For any issues accessing these materials, please contact the corresponding authors.
B. Supplementary Pareto Plots
The full set of Pareto plots are given below.
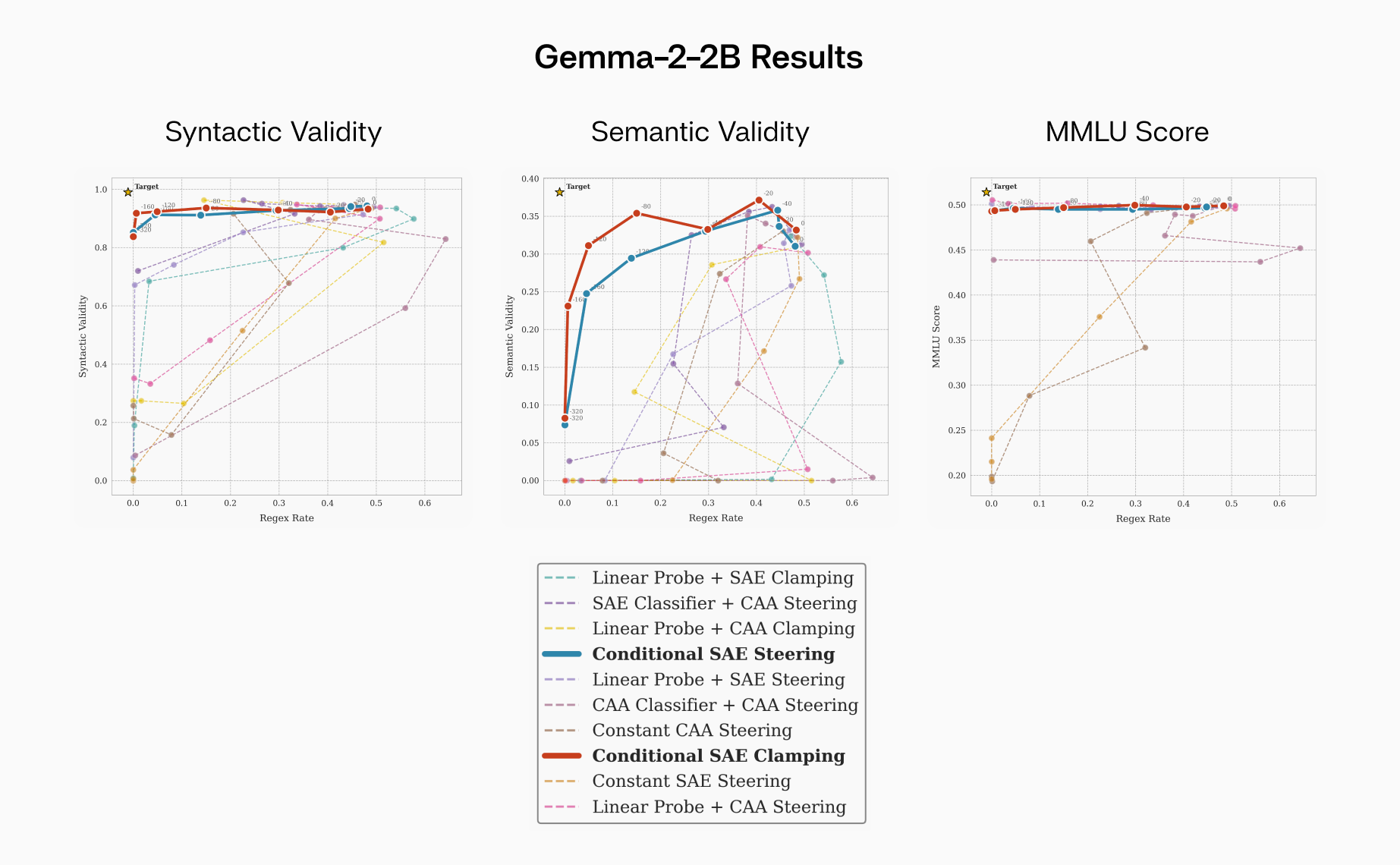 FIGURE 3: Gemma 2 2B IT results demonstrate the dominance of conditional SAE steering. These methods have minimal impact on MMLU score while consistently having the highest semantic validity for a given regex rate.
FIGURE 3: Gemma 2 2B IT results demonstrate the dominance of conditional SAE steering. These methods have minimal impact on MMLU score while consistently having the highest semantic validity for a given regex rate.
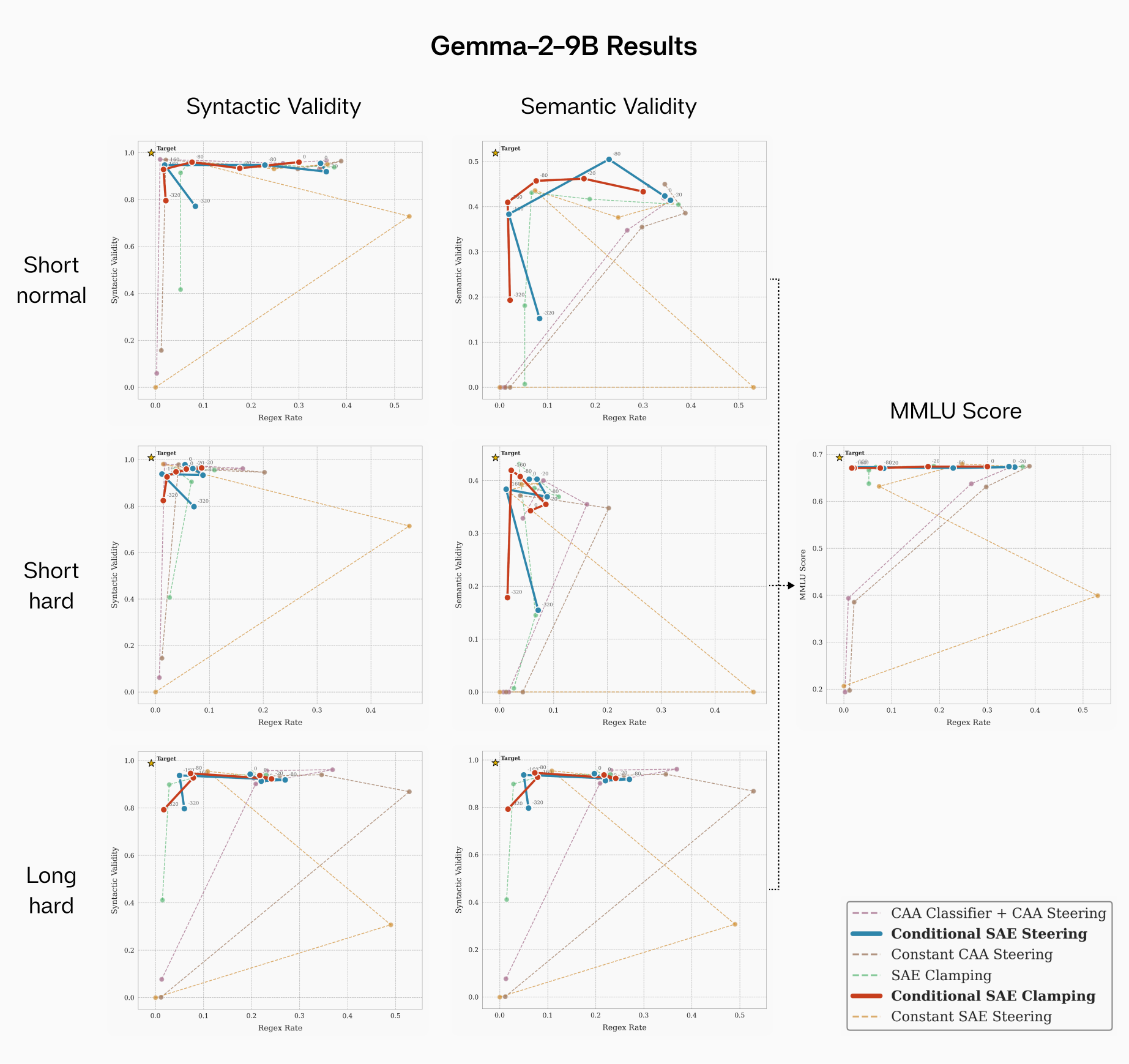 FIGURE 4: Gemma-2-9B-IT results across different prompt/context types. Even on prompts with hard regex constraints, conditional SAE clamping/steering improves performance without compromising MMLU. The benefit is also stronger at longer contexts.
FIGURE 4: Gemma-2-9B-IT results across different prompt/context types. Even on prompts with hard regex constraints, conditional SAE clamping/steering improves performance without compromising MMLU. The benefit is also stronger at longer contexts.
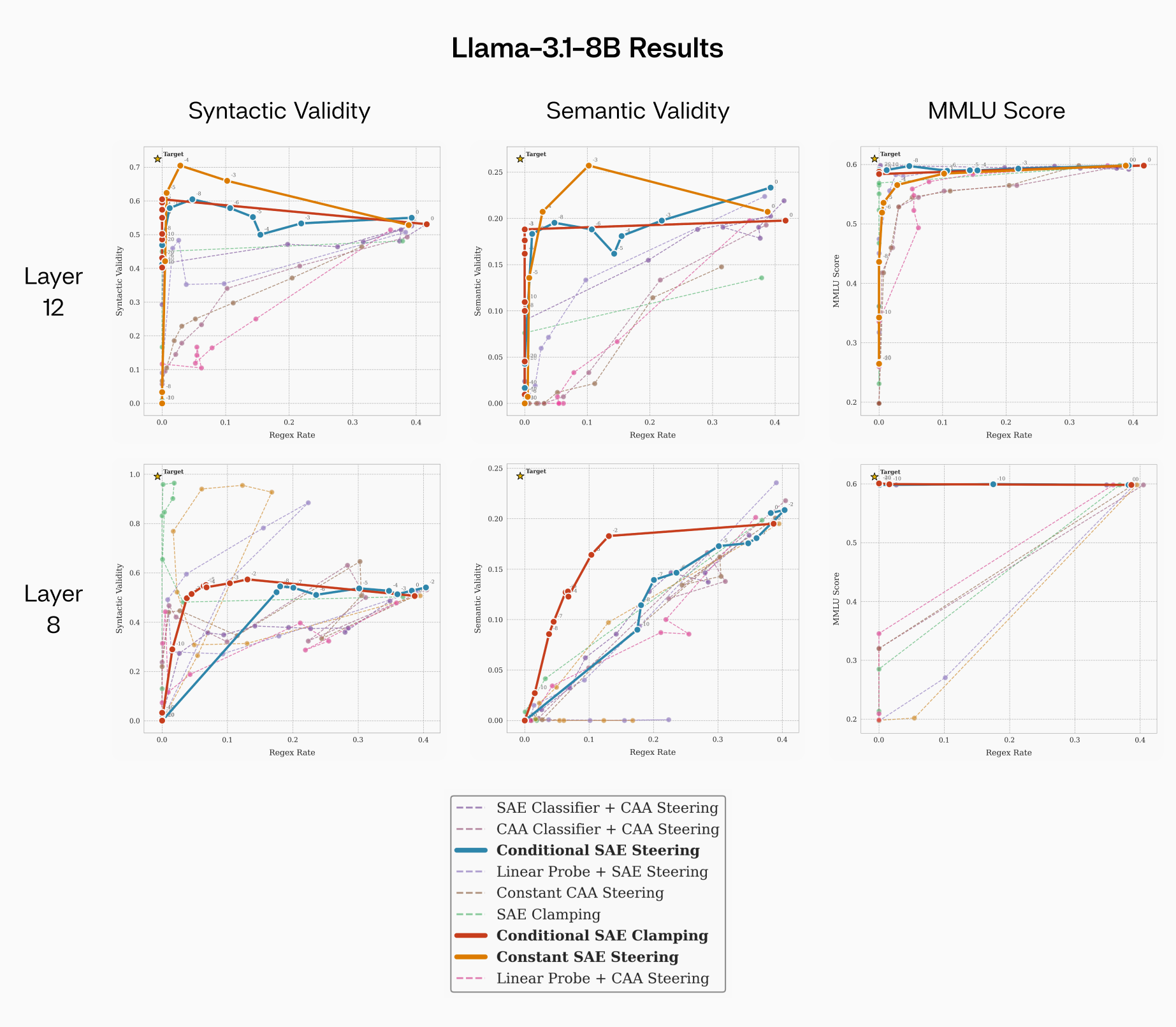 FIGURE 5: Llama-3.1-8B-Instruct results for features from different layers. Of note, constant SAE clamping/steering performs best for layer 12, which may be due to the decoder vector doing most of the work. For layer 8, conditional SAE clamping does much better than conditional SAE steering.
FIGURE 5: Llama-3.1-8B-Instruct results for features from different layers. Of note, constant SAE clamping/steering performs best for layer 12, which may be due to the decoder vector doing most of the work. For layer 8, conditional SAE clamping does much better than conditional SAE steering.
C. Addressing Alternative Approaches
While our SAE-based solution proved effective, two common alternatives warrant discussion: LLM-based output monitoring and model fine-tuning. We discussed these approaches with Max Von Hippel, Benchify's CTO, to understand why they weren't pursued.
LLM-Based Output Monitoring
"These errors reduce the quality of our output but are not, in general, totally catastrophic, so we'd rather not add more runtime through potentially cascading subsequent LLM calls... I should say that we have experimented with an LLM-judge kind of approach before, where we pipe the output of the code-gen model into another cheaper model that tries to correct certain errors, and I don't think it works very well. We run into the problem I mentioned earlier where you fix one bug and introduce another."
— Max Von Hippel, CTO of Benchify
Fine-Tuning Approach
"We want to avoid making or fine-tuning our own models since we think future model releases will solve most of our problems. I would add the caveat that if we don't get much better models in the next 6 months, we will try fine-tuning and see what it buys us. But I'd rather avoid it if possible... we will get around to trying it, but have had more important engineering problems to solve... Collecting good data in our domain is pretty tricky."
— Max Von Hippel, CTO of Benchify
Prompt Engineering Limitations
We explored prompt engineering, including adding multiple paragraphs to avoid regex usage (the "hard" prompt). However, Max's experience highlights the limitations of this approach:
"[T]he regex problem is one of a list of maybe 15 or so vaguely annoying mistakes that the LLMs routinely make, and in manual experiments, we've found that prompting to fix one of them can lead the LLM to make another, particularly for weirder problems where the LLM does not 'know' as many ways to achieve its directive. So we risk going on a wild goose chase."
— Max Von Hippel, CTO of Benchify
D. Generalization to Long Context
One of the most compelling advantages of our SAE-based approach emerges when dealing with long-context scenarios. We conducted experiments using Gemma-2-9B-IT with more extensive documentation added into the context. The plot is given above in Appendix B.
Our findings reveal a critical insight: even with explicit instructions, Gemma-2-9B-IT tends to ignore these directives at zero intervention strength when handling long-context inputs. While CAA steering vectors demonstrated reasonable effectiveness in short-context scenarios (as shown in our main results), their performance deteriorates significantly in long-context situations.
In contrast, SAE clamping/steering maintains robust performance across context lengths, highlighting its superior generalization capabilities. This resilience to context length variation represents a significant practical advantage for real-world applications where input length can vary substantially.
E. Evaluation Details
In this section, we describe our methods for evaluating generated code along three dimensions: regex usage, syntactic validity, and semantic validity. For MMLU evaluations, we used Eleuther's LM Eval Harness directly.
Code Extraction
For each generation, we first extract Python code blocks using the following pattern:
def extract_python(response):
pattern = r"python\s*(.*?)\s*"
match = re.search(pattern, response, re.DOTALL)
return match.group(1) if match else None
Regex Usage Detection
We detect regex usage by searching for common regex function calls. Manual inspection confirmed that regex usage was predominantly captured by these function patterns:
def check_for_re_usage(code_snippet):
pattern = r"\bre\.(match|search|sub|findall|finditer|split|compile|fullmatch|escape|subn)\b"
return bool(re.search(pattern, code_snippet))
Notably, we check for actual regex function usage rather than just re module imports, as intervened models would sometimes import the module without using it.
Syntactic Validity
For syntactic validity, we parse the abstract syntax tree:
def is_syntactically_valid_python(code):
try:
ast.parse(code)
return True, None
except SyntaxError as e:
return False, f"Syntax error: {str(e)}"
While this provides a basic correctness check, we found it to be an imperfect proxy for intervention success. For instance, code consisting entirely of comments would pass syntactic validation while being functionally useless.
Semantic Validity
For semantic validation, we create a restricted execution environment with access to basic Python utilities and the original function. We then verify that the generated code:
- Successfully compiles,
- Executes without errors, and
- Actually calls the target function
You can find the full implementation in our source code.
This validation runs with a timeout and in a sandboxed environment to prevent harmful operations. However, it's important to note that semantic validity does not evaluate the quality or coverage of the generated fuzz test—it only verifies basic execution correctness.
F. Classification Precision Analysis
A critical aspect of our investigation was quantifying the classification power of SAE encoder vectors. Given the Pareto dominance demonstrated by conditional SAE methods, we hypothesized that encoder vectors would exhibit superior classification precision compared to traditional linear probes.
Dataset and Methodology
We conducted extensive testing using:
- 700 model generations across 7 regex-related prompts
- 1400 generations across 14 non-regex prompts
Our goal was to identify intervention thresholds that maximize true positives while minimizing false activations.
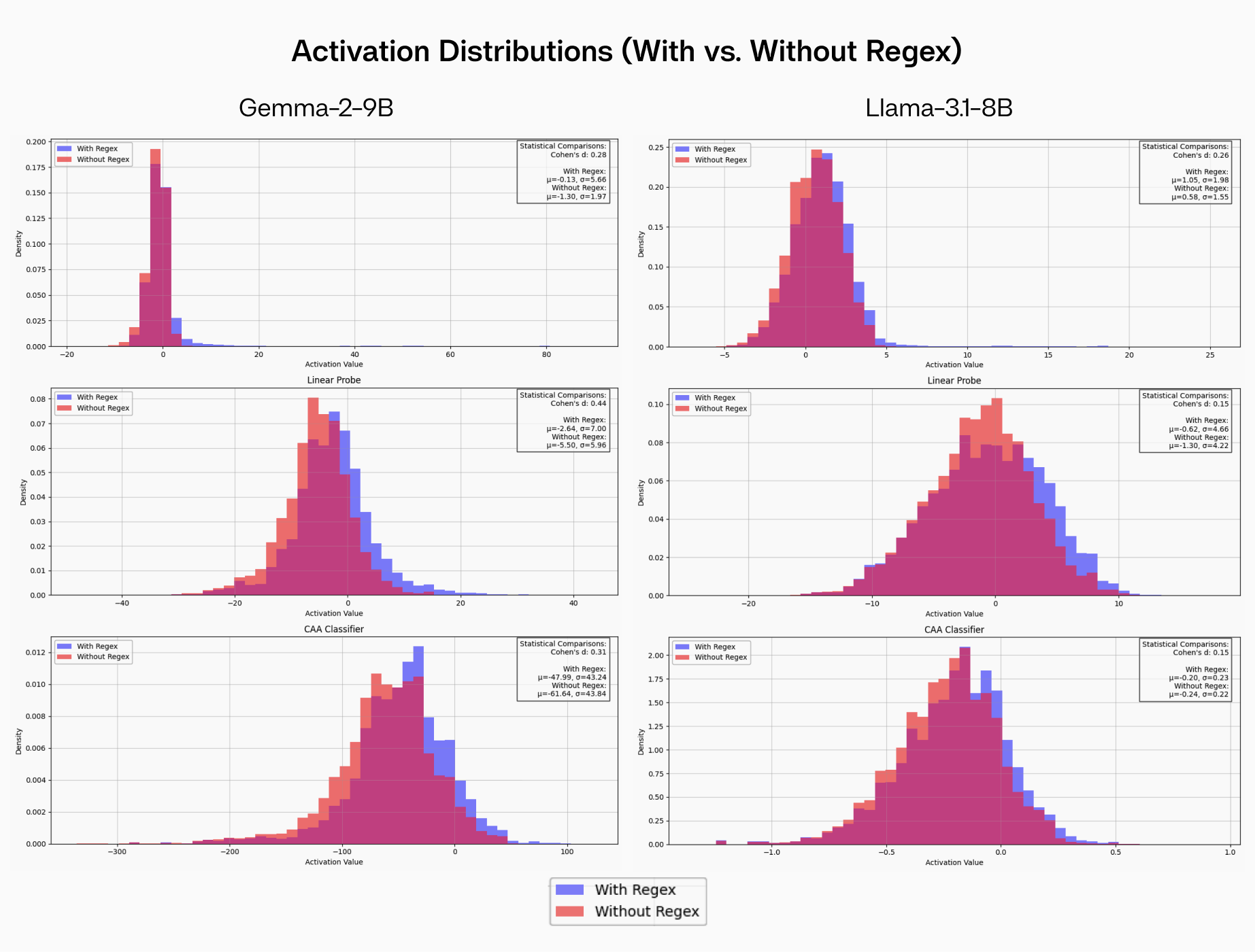 FIGURE 6: Activation value distributions across different classifiers, for both Gemma-2-9B-IT and Llama-3.1-8B-Instruct. Note the distinctive long-tailed distribution of SAE encoder vector activations (red) compared to linear probes (blue) and CAA steering vectors (green), suggesting more precise feature detection.
FIGURE 6: Activation value distributions across different classifiers, for both Gemma-2-9B-IT and Llama-3.1-8B-Instruct. Note the distinctive long-tailed distribution of SAE encoder vector activations (red) compared to linear probes (blue) and CAA steering vectors (green), suggesting more precise feature detection.
Measurement Considerations
Our precision-recall analysis revealed some interesting nuances:
-
Limited Recall Range: The curves show unusually low recall values (≤0.05) due to our labeling methodology:
- When regex appears in generated code, all tokens in the 1500-token sequence are labeled as "regex-related"
- However, the model only actively "considers" regex usage at specific decision points
- This noisy labeling means even perfect classifiers would show artificially low recall
-
Precision Measurement Challenges:
- Ground truth for model "consideration" of regex usage is unavailable
- False positives may include cases where the model contemplated but didn't implement regex
- Our string-matching detection can only identify actual regex usage, not consideration
Despite these measurement limitations, the SAE encoder vectors consistently demonstrated superior classification precision, aligning with their strong performance in the intervention experiments.
G. CAA Steering Vectors
CAA relies on a set of positive and negative completions and computes the difference between the centers of mass of the positive activations point cloud () and the negative activations point cloud () respectively.
Unfortunately, extracting an effective CAA is finicky, and relies on carefully curating the prompt for negative and positive examples. We had to experiment with the setup for several hours before arriving at an effective scheme.
For our CAA steering vectors, the setup we finally converged on was:
- A base instruction to write a fuzzing function
- A positive variant explicitly requesting regex usage
- A negative variant with no additional constraints
This allowed us to generate clean contrastive examples while minimizing confounding variables:
{
"base": "Write a custom python fuzzing function to test the provided code.",
"pos": "Use regular expressions in your test.",
"neg": ""
}
H. Linear Probe Training
Dataset Construction
We developed a carefully controlled dataset for training linear probes, consisting of:
- 7 distinct prompts with example functions
- 2 response conditions per prompt:
- Explicit instruction to use regular expressions
- Explicit instruction to avoid regular expressions
- 50 generations per condition (400 tokens each)
- Total dataset size: 700 examples (7 × 2 × 50)
The dataset was constructed from the following setup:
{
"base": "Write a custom python fuzzing function to test the provided code.",
"pos": "Use regular expressions in your test.",
"neg": "Absolutely do not use regular expressions in your test."
}
Training Parameters
- We used a standard 80-20 train-test split
- Model performance:
- Gemma-2-9B-IT: 86% test accuracy
- Gemma 2 2B IT: 80% test accuracy
- Llama-3.1-8B-Instruct: 83% test accuracy
Methodology Considerations
We intentionally kept prompts concise and verified instruction adherence through manual inspection. This approach ensured:
- Clear binary classification targets
- Reliable ground truth labels
- Minimal confounding variables
Limitations and Challenges
The moderate accuracy levels of our linear probes can be attributed to an inherent labeling challenge.
Ideal vs. Available Labels:
- Ideal: Label only tokens where the model "considers" regex usage
- Reality: Must label entire generations as positive/negative
Without sophisticated tools like sparse autoencoders, we cannot identify the tokens where the model "considers" regex usage. Instead, we must label entire generations as either positive or negative examples, introducing substantial noise into our training data. This coarse labeling scheme, while necessary given our constraints, likely limited the probe's ability to learn fine-grained patterns in the model's behavior.
I. Quantitative Differences between Llama and Gemma Models
Our experiments revealed significant differences in clamping/steering behavior between Llama and Gemma models, particularly in two key areas: semantic validity impact and intervention scale requirements.
Semantic Validity Response
A notable distinction emerged in how constant steering affected semantic validity:
- Llama Models: Showed minimal changes in semantic validity under constant steering, though MMLU scores decreased significantly
- Gemma Models: Exhibited more pronounced changes in semantic validity
We propose two potential explanations for this difference:
- Llama may be inherently more amenable to SAE-based interventions
- Our Llama Code SAEs, trained primarily on code-specific datasets, might produce higher-quality interventions
Intervention Scale Requirements
We observed substantial differences in the magnitude of intervention required:
| Model Family | Typical Intervention Range |
|---|---|
| Llama | -2 to -10 |
| Gemma | -20 to -200 |
Despite normalizing decoder vectors before intervention, this order-of-magnitude difference persists. The underlying cause remains uncertain and warrants further investigation.
J. Qualitative Effects of Increasing Constant Steering Intervention Magnitude
With interventions that are constantly applied, it is often not the case that increasing the intervention strength strictly decreases regex usage with a clean inverse relationship. Instead, we often see multiple phases.
Note: All example model outputs are real Gemma-2-9B-IT generations from our experiments.
Phase 1: Expected Behavior
Initially, increasing the negative intervention leads to the desired outcome: reduced regex usage. The model produces clean, appropriate code like:
import pytest
def test_obfuscate_credit_cards_fuzz():
# A fuzz test for obfuscating credit card numbers
for _ in range(1000):
text = ''.join(chr(random.randint(33, 126)) for _ in range(random.randint(10, 50)))
result = obfuscate_credit_cards(text)
assert '****-****-****' in result
Phase 2: Counterproductive Response
Surprisingly, further increasing the negative intervention sometimes triggers a dramatic increase in regex usage. This is dependent on specific model and prompt combinations and doesn't always happen. The model becomes unstable and fixates on regex patterns, producing code like:
import re
re.configure_transaction(text: str) -> tuple:
text = re.sub(r'\b(?:\d{4}[-\s]?){3}\d{4}\b', lambda m: '****-****-****-' + m.group(0)[-4:], text)
Phase 3: Complete Breakdown
At the highest intervention levels, the model's output becomes entirely incoherent. It produces nonsensical text that bears no relation to the task, such as:
4.12. Family members is a valuable asset for.